|
A
logarithmic image transformation
Jos
Leys
Abstract :
An
image
transformation method, first used by the artist M.C. Escher, and
described by
Lenstra et al. is generalized for use in a graphics program.

Figure
1:
Escher's "Printgallery"[1] |
In
1956, Maurits Cornelis Escher
completed a drawing called “Print Gallery”. The
drawing depicts a young man
looking at a print in a gallery that is deformed almost beyond
recognition.
There is an enigmatic white area in the center of the image.
In
2003, a group of
mathematicians at Leiden University,
led by Prof. Hendrik Lenstra succeeded in unraveling the mathematical
structure
of the image.[2]
Once
this structure was known, they could ‘complete’ the
image by filling in the
famous white spot with the help of a computer algorithm.
A
summary of their method was
published in a paper [3]
, and
received a lot of acclaim, not only in academic circles, but also in
the
general press.
|
In this article I will
show how
Lenstra’s method can be applied more generally for the
transformation of
images, and the generation of endless zoom animations.
The
transformation consists of
three stages, which will be described hereunder:
Stage 1: transformation by $\log(z)$. (
base
e
logarithm).
The transformation $z
\mapsto \log(z)$
will transform the complex plane in a strip running from $-\infty$ to
$+\infty$ along
the real axis with a width equal to 2$\pi$:
any point on the complex plane can be represented as $re^{i\theta}$,
so $\log(z)=\log(r)+i\theta$. As $0\leq\theta\leq2\pi$,all
points will be transformed to a strip of width $2\pi$.
However as $re^{i\theta}=re^{i(\theta+n2\pi)}$ for any integer
$n$, any parallel strip between $n2\pi$ and
$(n+1)2\pi$ can be considered as an image of the complex plane: in
other words, $\log(z)$ will transform the complex plane into
an infinite number of copies..
For our image transformation, let’s consider how
$\log(z)$ transforms the area between a set of concentric circles of
radius $r_1$ and $r_2$. ( Fig. 2).
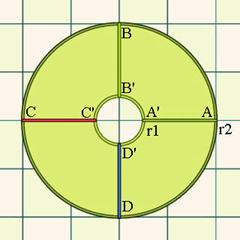
Figure
2: Concentric circles. |
|
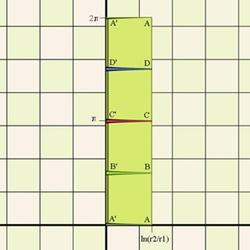
Figure
3: Circles transformed by $\log(z)$. |
The transformation illustrated in Figs. 2 and 3 is the transformation
$z\mapsto \log(\frac{z}{r_1})$ . The outer circle becomes a vertical
line at $\log(\frac{r_2}{r_1})$ , and the inner circle is
transformed to a vertical line at zero: we have cut the disc of Fig. 1
along line A’-A, and bent it into a rectangle.
Stage 2:
Rotation and scaling.
The rectangle in Fig.3 is now rotated so that its diagonal
coincides with the imaginary axis, and the rectangle is shrunk so that
the diagonal is equal to 2$\pi$. In transformation terms, this is equal
to $z\mapsto zfe^{i\alpha}$, with
$\alpha=\arctan(\frac{\log(r_2/r_1}{2\pi})$ and $f=\cos(\alpha)$ .
(Fig. 4)
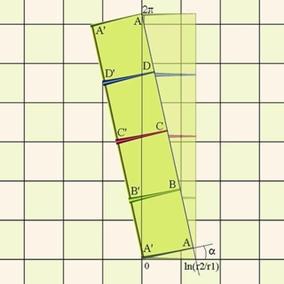
Figure
4: rotation and scaling |
In the next stage we will do the transformation that is the
inverse of the log transformation of phase 1.
Stage 3:
exponentiation.
We will now transform the rectangle of Fig.4 with the
transformation $z\mapsto e^z$ . This produces the image in Fig. 5:
All the sides of the
rectangle of Fig. 4 are transformed into spirals. Notice that points A
and A’ now coincide, as they were transformed from
$2\pi i$ and $0$ respectively, which both transform to $1$.
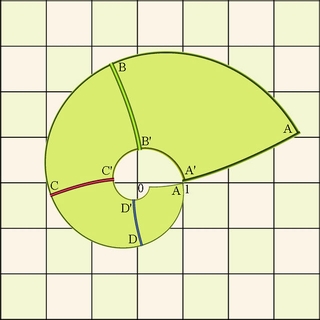
Figure
5: Exponential transformation. |
This concludes the basic transform.
Combining all the stages, the transformation becomes
$$z\mapsto (\frac{z}{r_1})^\beta,$$ where $\beta=fe^{i\alpha}$.
The original image of two concentric circles will be transformed into
an identical image by the transformation $z\mapsto
\frac{z}{r_2/r_1}$, so for the transformed image, an identical copy is
obtained if z is divided by $(\frac{r_2}{r_1})^\beta$ .This means a
scaling by $|(\frac{r_2}{r_1})^\beta|$ and a
rotation by minus the argument of $(\frac{r_2}{r_1})^\beta$.
We now go back to stage 2. We replicate the rectangle of Fig. 4 so that
it tiles the plane, and then do the stage 3 transformation again.
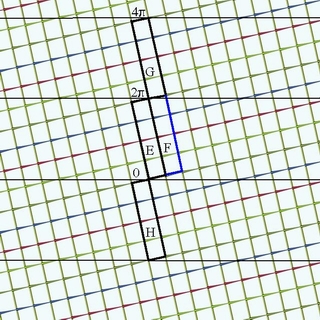
Figure
6: Tiling |
|
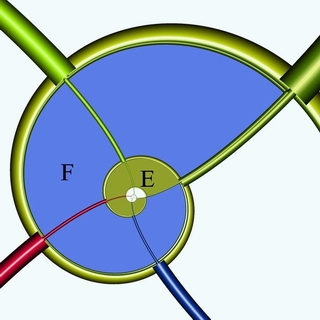
Figure
7: Exponentiation of the tiling |
Rectangle ‘E’ in Fig. 6 is the original
rectangle of Fig. 5, and is transformed by stage 3 to the area
‘E’ in Fig. 7. Rectangle ‘G’
and ‘H’ will also be transformed to area
‘E’. Rectangle ‘F’ will be
transformed to area ‘F’ in Fig. 7. We thus obtain
an infinite number of replicas of the original image, transformed so
that they tile in spiral form in a seamless fashion. All the replicas
are self-similar: area ‘E’ in Fig.7 can be enlarged
and rotated to cover area ‘F’ exactly.
The configuration of stage 2, where the rectangle is rotated and scaled
so that the diagonal is vertical, and equals 2$\pi$ is not the only one
possible. All possible configurations are shown in Fig.8. If the
rotation is 0° or 180° and the scaling factor equals 1,
the transformation will produce an infinite number of concentric copies
of the original image. In all other cases, the scaling equals
$f=\cos(\alpha)$ ,and the rotation equals $\alpha$ ,
$\pi-\alpha$, $\pi+\alpha$, or -$\alpha$.
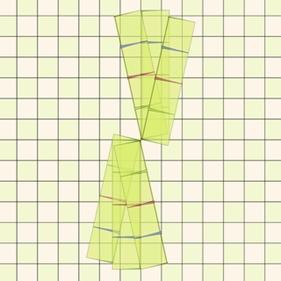
Figure
8: Possible configurations |
In summary, the transformation logic is as follows:
- Choose $r_1$ and $r_2$ ( a slight adaptation is necessary
to allow circle centers different from the origin).
- Calculate $\alpha$, $f$, and $\beta$ .
- Calculate $\beta \log(z/r_1)$ for the area
between
the circles, tile the resulting rectangle, and finally
calculate $e^{\beta \log(z/r_1)}$ for all pixels.
The transformation was
implemented in Ultrafractal [4],
a graphics
program that features user defined algorithms, and some examples follow
below:

Figure
9: image 1, original |

Figure
10: image 1, transformed |

Figure
11: image 2, original |

Figure
12: image 2, transformed |

Figure
13: image 3, original |

Figure
14: image 3, transformed |
The algorithm can be adapted to allow for non-concentric
circles, or even non-concentric polygons.
The area between the two squares in Fig. 15a is transformed by the log
transformation into the shaded area in Fig. 15b. This area is then
tiled taking into account the angle offset between the two squares.
After exponentiation, Fig. 15c is obtained. With a rotation of the
tiling after the log transformation, the outcome is Fig. 15d.

Figure 15a |

Figure 15b |

Figure 15c |

Figure 15d |
One can zoom in or out on the transformed images indefinitely.
The value of $\beta$ can be calculated from the size ratio of
the small image vs. the large, and this allows to calculate the
magnification and rotation needed to obtain an image that is identical
to the start image. A limited number of frames thus suffices to obtain
and endless zoom movie, provided the video file is shown in loop mode.
Fig.16 shows such a zoom movie. ( A “Droste
effect” movie)
Fig.17 shows anarrangement
whereby the smaller square is off-center versus the large
square. We now need to calculate the fixed point of the transformation.
With $C_L$ =center of large square, $C_S$=center of small square,
$\theta$ = offset angle between the two squares and $m$ = ratio of the
side of the small square vs. the large square, the fixed point $C_F$ is
given by:
$$C_F=C_L+\frac{(C_L-C_S)}{(1-me^{i\theta})}$$
The log transform then
takes the form $z\mapsto \log( \frac{(z-C_F)}{a})$ with $a$ = the
shortest distance from $C_F$ to the edge of the small square.
The overall transform becomes $z\mapsto (\frac{(z-C_F)}{a})^\beta$,
where $\beta=fe^{i\alpha}$, with
$f=\frac{2\pi}{(2\pi-\theta)}\cos(\alpha)$,
$\alpha=\arctan(\frac{\ln(m)}{2\pi})$ .
An identical copy is achieved through a scaling and rotation by the
absolute value and the argument of
$\Large m^{\frac{fe^{i(\alpha-\phi)}}{\cos(\phi)}}$ with
$\phi=\arctan(\frac{\theta}{\log(m)})$.

Figure 17a |

Figure 17b |

Figure 17c |
Figure 17d |
The figures below show
some examples.

Figure
19: “LW346” by M.C.
Escher[1] |

Figure
20: Transformed image |

Figure
21: Original |

Figure
22: Transformed |
Fig. 23 shows frames from a ‘Droste
effect’
animation based on a vintage airline poster.
Finally, the transformation can also be applied to any shape.
In this
case, the shape in question has to be made fully transparent. One can
then have the algorithm find the rim of the shape by reading
the alpha channel of the image file. The alpha channel value for a
transparent pixel is zero, so a simple algorithm can find the location
of the rim. Figure 24 shows a sequence of images to illustrate this:
The area in the picture on the wall in the image on the right is first
made transparent, as to obtain the middle image. One then chooses a
point in the transparent area, and a size factor. This will then create
a similar area outside the transparent area (which may be rotated
versus the transparent image)., as in the image on the right.
This can then create the following images:
Below are some other examples of free-form image shapes.
 |
 |
| Figure 26 |
Professor Lenstra and his team proved that the M.C. Escher
Print Gallery image has a ratio $m=\frac{r_2}{r_1}=256$ . This means
that the rotation angle for stage 2 is
$\alpha=arctan(\frac{\log(r_2/r_1}{2\pi})$ or
41.429..…degrees, and the scale factor
$f=\cos(\alpha)$ or 0.749767… . .
With $\beta=fe^{i\alpha}$,
$|(\frac{r_2}{r_1})^\beta|$ = 22.5836…, and the argument
of $|(\frac{r_2}{r_1})^\beta|$ is
157.62559…degrees, so an identical image is obtained by
zooming by a factor of 22.5836…and a rotation by
-157.62559…degrees.
It is amazing that M.C. Escher drew his Print Gallery by intuition, as
he was “untrained in mathematics”.[5]
Yet, his
image is very close to the computer generated image, based on the above
algorithm. It is also known that Escher spent a very long time on this
drawing. It makes one wonder what he could have done with a computer.
References
[1]
©
2006 The M.C. Escher
Company, the Netherlands. All rights reserved.
Used by permission.
[2] Escher
and the Droste effect. http://escherdroste.math.leidenuniv.nl/.
[3]
B. de Smit and H. W.
Lenstra Jr:
The
mathematical structure of
Escher’s Print Gallery. Notices of the AMS, Volume
50, number
4.
[4]
Ultrafractal
by Frederik Slijkerman
[5]
The MacTutor
History of Mathematics archive.
(webpage)
| 
