The hyperbolic chamber

Jos Leys

This article was first published (in French) on "Images des Mathématiques, a website of the CNRS (Centre National de Recherche Scientifique), December 2008.

The geometry that we have all learned in school is the Euclidian geometry, based on a certain number of axioms that Euclid described in his great book "The Elements". The fifth axiom is the "parallels" axiom: through a point outside of a straight line runs one, and only one straight line that is parallel to the straight line.

Is it possible to imagine a geometry where all the axioms are valid except for the fifth one? This question preoccupied a lot of mathematicians and was answered in the beginning of the 19th century. Lobachevsky, Bolyai and Gauss proved that this is indeed possible: they described a coherent geometry without the parallel axiom, and called it "hyperbolic geometry". This geometry was initially just an intellectual creation, without real application, but has gained more and more importance in mathematics, to the point where certain mathematicians now have a real intuition for it, as if they really lived "inside" this geometry. As an example, hyperbolic geometry in three dimensions has been key to putting the famous Poincaré conjecture in a natural context, which led to the magnificent solution by Perelman of the geometrisation conjecture in 2006.

The question we will try to answer in this article is this : How could a science museum give its visitors a concrete idea of hyperbolic geometry?

To try and answer that question, let us briefly explain some basic notions on the subject of a geometry where an infinity of parallel lines can be drawn through a point outside a line.

Remark

There are different models to represent hyperbolic geometry in a Euclidian setting. We will only show the "Poincaré disc" model.

The (hyperbolic) plane is represented by the interior of the (Euclidian) unit disc. This means that points outside the disc, that we can see because we live in the Euclidian world, do not belong to the universe of the hyperbolic plane, and the inhabitants of the hyperbolic plane ignore these points. In this model "(hyperbolic) straight lines" are  arcs of circles that are orthogonal to the unit circle.

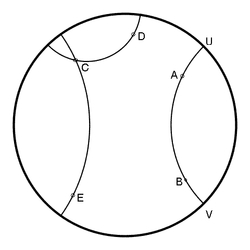The figure on the left shows the "hyperbolic straight lines" connecting the points $A$ and $B$, $C$ and $D$ and finally $C$ and $E$. The Euclidian circle arcs $CD$ and $CE$ do not intersect the arc $AB$, which means that $CD$ and $CE$ are parallel to $AB$. Two straight lines are parallel if they do not intersect (or if they coincide). In Euclidian geometry, two straight lines that are parallel to a third line are parallel. This is clearly not the case in hyperbolic geometry, and so our intuition is not a good guide here. What we are also used to, is that two parallel lines are everywhere at the same distance from each other, but in hyperbolic geometry, this is not true either. The hyperbolic distance $\bar{d}$ between points A and B can be defined by $$ \bar{d}=\frac{1}{2}\left|\ln{\left(\frac{AV.BU}{AU.BV}\right)}\right|$$

$AV, BU, AU, BV$ are the (Euclidian!) distances between the points. If either $A$ or $B$ approach $U$ or $V$ then this distance becomes infinitely large: the rim of the disc is not part of the Poincaré disc, it is called the horizon "at infinity".

Where does this formula come from?

The Euclidian plane has the metric $ds=\sqrt{dx^2+dy^2}$. In the Poincaré disc, this metric can be defined as $ds=\frac{\sqrt{dx^2+dy^2}}{1-x^2-y^2}$. When one approaches the rim, distances become 'longer'. We wish to calculate the distance between points $A$ and $B$ in the figure on the left. $A$ and $B$ are both on a hyperbolic straight line, which is a Euclidian circle arc of radius $R$. To calculate the distance, we need to integrate $ds$ on this circle between $B$ and $A$. For any point $P$ on the circle, we measure the angle $\theta$ between the line segments $PM$ and $OM$. We call $\phi$ the angle $O\hat{M}U$. We have $x=OM-R\cos{\theta}$ and $y=R\sin{\theta}$, from which $dx=R\sin{\theta}d\theta$, $dy=R\cos{\theta}d\theta$. We need to calculate $$\bar{d}=\int_{\theta_{B}}^{\theta_{A}}{\frac{Rd\theta}{1-(OM-R\cos{\theta})^2-R^2\sin^2{\theta}}}$$ Given that $OM^2=1+R^2$ and $OM=\frac{R}{\cos{\phi}}$, $$\bar{d}=\frac{\cos{\phi}}{2R}\int_{\theta_{B}}^{\theta_{A}}{\frac{d\theta}{\cos{\theta}-\cos{\phi}}}$$. Some useful trig formulas: $$\cos{\theta}-\cos{\phi}=2(\cos^2{\frac{\theta}{2}}-\cos^2{\frac{\phi}{2}})=-2(\tan^2{\frac{\theta}{2}}-\tan^2{\frac{\phi}{2}})\cos^2{\frac{\theta}{2}}\cos^2{\frac{\phi}{2}}$$ Put $$t=\frac{\tan{\theta/2}}{\tan{\phi/2}} , dt=\frac{d\theta}{2\tan{\frac{\phi}{2}}\cos^2{\frac{\theta}{2}}}$$ The integral becomes: $$\bar{d}=\frac{\cos{\phi}}{2R\cos^2{\frac{\phi}{2}}\tan{\frac{\phi}{2}}}\int_{\theta_{B}}^{\theta_{A}}{\frac{dt}{1-t^2}}$$ $$\bar{d}=\frac{\cos{\phi}}{R\sin{\phi}}\int_{\theta_{B}}^{\theta_{A}}{\frac{dt}{1-t^2}}$$ $$\bar{d}=\int_{\theta_{B}}^{\theta_{A}}{\frac{dt}{1-t^2}}$$ because $R\tan{\phi}=1$. So we obtain: $$\bar{d}=\frac{1}{2}\left[\ln{\left(\frac{1+t}{1-t}\right)}\right]_{\theta_{B}}^{\theta_{A}}$$ $$\bar{d}=\frac{1}{2}\left[\ln{\left(\frac{1+\frac{\tan{\theta/2}}{\tan{\phi/2}}}{1-\frac{\tan{\theta/2}}{\tan{\phi/2}}}\right)} \right]_{\theta_{B}}^{\theta_{A}}$$ $$ \bar{d}=\frac{1}{2}\left[\ln{\left(\frac{\sin{\frac{\phi+\theta}{2}}}{\sin{\frac{\phi-\theta}{2}}}\right)} \right]_{\theta_{B}}^{\theta_{A}}$$ $$\bar{d}=\frac{1}{2}\ln{\left(\frac{\sin{\frac{\phi+\theta_{A}}{2}}}{\sin{\frac{\phi-\theta_{A}}{2}}}\right)}-\frac{1}{2}\ln{\left(\frac{\sin{\frac{\phi+\theta_{B}}{2}}}{\sin{\frac{\phi-\theta_{B}}{2}}}\right)}$$ As angles are measured relative to the line segment $OM$, the sign of $\theta$ is positive if the point is above this segment, and negative if it is below. The Euclidian distances are as follows: $$AU=2R\sin{\frac{\phi-\theta_{A}}{2}}$$ $$AV=2R\sin{\frac{\phi+\theta_{A}}{2}}$$ $$BU=2R\sin{\frac{\phi+|\theta_{B}|}{2}}$$ $$BV=2R\sin{\frac{\phi-|\theta_{B}|}{2}}$$ $$\bar{d}=\frac{1}{2}\ln{\left(\frac{AV.BU}{AU.BV}\right)}$$ To avoid that this distance becomes negative, we have to take the absolute value: $$\bar{d}=\frac{1}{2}\left|\ln{\left(\frac{AV.BU}{AU.BV}\right)}\right|$$

In order to give the museum visitor the illusion that he finds himself in a hyperbolic world, we would need to put him/her on a disc so that the rim is invisible as it is infinitely far away. We would also need to give visitors the illusion that lightbeams follow paths that are circle arcs instead of straight lines. All this is not easy! Let us first look at some other properties of hyperbolic geometry. 

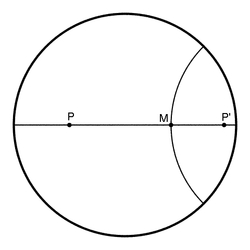In the image on the left, points $P$ and $P'$ are symmetrical  vs. the hyperbolic straight line passing through the point $M$ and perpendicular tp $PP'$. The hyperbolic distances $\bar{MP}$ and $\bar{MP'}$ are identical. We are of course refering to hyperbolic symmetry, and not a Euclidian one! One can verify, using the hyperbolic distance formula, that the point $P'$ is obtained by inversion in the circle representing the hyperbolic straight line passing through $M$ and perpendicular to $PP'$. If $C$ is the center of this circle we have $$CP'=\frac{R^2}{CP}$$

More about inversion.

In the following figure, inversion in the circle of radius $R$ and center $C$ transforms the point $P$ in the point $P'$ such that $P$, $P'$ and $C$ are aligned and $CP.CP'=R^2$. .This transformation is conformal: angles are preserved. In the figure below, all the lines in the square are transformed in circle arcs that intersect orthogonally. Inversion transforms circles into circles (taking into account that straight lines are circles with infinite radius). Note that the center of a circle is not transformed in the center of the inversion image circle. The equivalent in three dimensions is the inversion in a sphere. In the figure below, the point $P$ is transformed by inversion in the sphere of radius $R$ and center $C$ to the point $P'$, with $CP.CP'=R^2$. Just as inversion in a circle transforms circles to circles, inversion in a sphere transforms spheres to spheres ( but without sending center to center).

Let's apply this notion of symmetry to tilings. If we want to pave the Euclidian plane with regular polygons, we have the choice between triangles, squares and hexagons. With triangles, six will meet at each vertex. With squares, the number is four, and with hexagons it is three, as in the figures below..

In our hyperbolic plane, the situation is quite different. To start with, the sum of the angles of a triangle is not equal to $\pi$ anymore: the sum is always smaller than $\pi$.

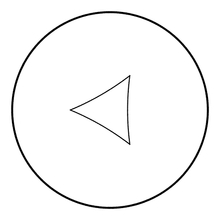On the left is an equilateral triangle where the sum of the angles is $3\pi/4$ ( angles are measured by measuring the angles between the tangent lines). On the right is an equilateral triangle where the sum of the angles is close to zero. This means that one can draw equilateral triangles with any angles between $0$ and $\pi/3$, and that one can draw an infinity of tesselations by equilateral triangles. The same thing is true for the other regular polygons.

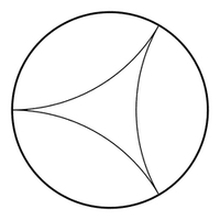How can we draw a tiling by regular (hyperbolic!) polygons with $n$ vertices so that $p$ polygons meet at each vertex?

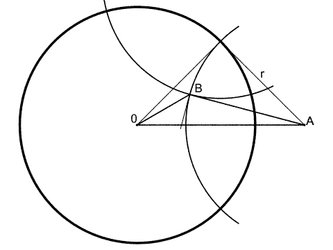In the figure on the left, we have to find the position of the center $A$ and the radius $r$ of a circle so that: the circle is orthogonal to the unit circle. The angle between this circle, and a second circle with the same radius, rotated by an angle $2\pi/n$ around the origin, equals $2\pi/p$. In the triangle $ABO$, the angle $\widehat{BOA}$ equals $\pi/n$, and the angle $\widehat{OBA}$ equals $\pi/p+\pi/2$. As $AO=\sqrt{1+r^2}$ and $AB=r$, we can easily find $r$ and $|OA|$.

This construction is only possible if $\frac{\pi}{n}+\frac{\pi}{p}+\frac{\pi}{2}<\pi$, from which follows the general rule for hyperbolic tilings: $$\frac{1}{n}+\frac{1}{p}<\frac{1}{2}$$

In order to draw the polygon, we rotate the point $A$ around the origin by an angle $2\pi/n$, and we draw the circle arcs of radius $r$. If we take $n=6$ and $p=4$, this gives us:

So this is a fundamental tile. As $p=4$, the angles of the polygon are all $\pi/2$. In order to find the neighbouring tiles, all we need to do is to draw the symmetric tiles in a hyperbolic way. The symmetry axes are the sides of the polygon. As we have seen, symmetry in the hyperbolic plane means inversion in a circle. The fact that the circle inversion is a conformal transformation, assures that the angles will be preserved, and the images by inversion (in the circles that make up the sides of the polygons) will also have angles of $\pi/2$. We obtain this picture:

And we can repeat this as many times as we want:

This is the tiling that M.C.Escher used in his famous "Cirkellimiet 4, Angels and Demons". Note that Escher carved this in wood by hand!

M.C.Escher took this tiling, but he obviously did not use the images of the tiles obtained by inversion. At each inversion, the image was turned 180° which assures that the demons and angels match up perfectly.
Here are two other examples. On the left the same (6,4) tiling, this time with triangles in alternating colors, and on the left a (3,18) tiling.

Back to the science museum. We now know how to tile the hyperbolic plane with tiles that are obtained by circle inversions. How does this help us for our construction in the museum?

Remember those "Galleries of Mirrors" with all sorts of mirrors that deform the reflection of the spectator into bizarre shapes?  In order to lose some weight all one needed to to was to stand in front of a cylindrical mirror with a vertical axis.

So here is our idea for the museum: We build a chamber where the walls are cylindrical mirrors. We choose the radii and positions of the mirrors as if we were constructing the base tile of a hyperbolic tiling.

Here is a what such a chamber might look like. ( At the moment, there are just two visitors, and we still have to construct a way in and out!)

Will the visitor's view in this chamber be exactly like the view in a real hyperbolic world? Unfortunately, no! Let's not forget that straight lines in the hyperbolic world, so lines that light beams will follow, are Euclidian circle arcs. This means for instance that a visitor in one corner of the room should be able to see all the other corners, and this is not the case! The chamber itself is not hyperbolic..

Nevertheless, it can be shown that the view inside the chamber, and all the reflections on the walls do not differ much from the view in a real chamber in a hyperbolic world. The mathematical explanation for this is outside the scope of this article.

Let's put our camera inside the chamber :

With good quality mirrors, the visitors will experience the illusion that they find themselves on an infinitely large plane, just like the inhabitants of the hyperbolic world, who cannot see the edge of the disc either.

For the shape of the chamber, the possibilities are endless. Here is a chamber accoring to the (3,100) tiling:

..and the view on the inside:

For comparison, here is a purely Euclidian chamber:

How can we make the experience even more spectalular for the visitors in the museum?

So far we we only talked about the hyperbolic plane, but we can also talk about hyperbolic space. Instead of Poincaré's disc, let's take Poincaré's ball, the interior of a unit ball in Euclidian space. In this ball, "hyperbolic planes" are pieces of spheres that are orthogonal to the unit sphere. Symmetries can now be described by inversions in these spheres.

This hyperbolic space can also be "tiled" by regular polyhedra. In our Euclidian world, the only regular polyhedron capable of  such a tiling is the cube, but in the hyperbolic world we have a choice! We will see that the choice is not as abundant as what we could in the hyperbolic plane. Note that the hyperbolic space that we are refering to is three-dimensional. One can also discuss higher dimensional hyperbolic spaces, and the possibilities to tile that space, but this would lead us too far ( more specifically, outside of the competence of this author!). Suffice it to say that it has been shown relatively recently that such a tiling is impossible in dimensions higher than 30, a theorem dating from 1983 by the Russian mathematician Ernest Vinberg.

Hyperbolic regular polyhedra are objects with faces that are pieces of spheres.

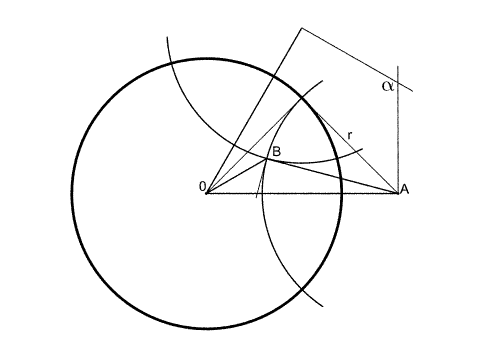Look at the figure on the left: this can be considered as a cut through the Poincaré ball by a plane passing through the origin. The angle $\widehat{BOA}$ is now equal to $(\pi-\alpha)/2$, with $\alpha$ the diedral angle of the Euclidian polyhedron. In order to be able to construct tilings where $p$ polyhedra meet at each edge, the condition is : $$\frac{\pi}{p}<\frac{\alpha}{2}$$ There is also a second condition:  the spheres that make up the faces of the polyhedron must be orthogonal to the unit sphere, which creates a maximum for $p$: for polyhedra where three faces meet at a vertex, the maximum value of $p$ is 6, for 4 faces this is 4, and for 5 faces it is 3.333..

All this limits the possibilities for tilings by hyperbolic regular polyhedra to the following:

• Tetrahedron with dihedral angles of 60° with "vertices" on the unit sphere ( a purist opnion could be that this is not really a polyhedron as the vertices are at infinity, and the inhabitants of the hyperbolic balls cannot see them!)
• Cube with dihedral angles 72° or 60°. In the latter case, the "vertices" are at infinity.
• Octahedron with dihedral angles 90°.
• Dodecahedron with dihedral angles 90°, 72° or 60° ( in the latter case the "vertices" are at infinity).
• Icosahedron with dihedral angles 120°.

For our museum, we could consider a chamber with spherical walls, arranged to obtain a tiling of hyperbolic space. here is a chamber in the shape of a hyperbolic cube:

Here is a view inside the chamber. Click here for a 360° panoramic view.

If you prefer a chamber in the shape of a dodecahedron:

..the view inside the chamber is this:

And finally an icosahedron project:

All that is left now is to convince a museum director to invest in such a project!

More information on the subject :

1. Non-Euclidian geometry.

2. The Poincaré disc.

3. "Curved spaces" by Jeff Weeks.

4. Hyperbolic tilings.