1. Introduction
The shape of the Earth has intrigued scientists throughout history. The general acceptance of the fact that the Earth is round came
about in the first century A.D., although Pythagoras had already postulated a spherical Earth 600 years earlier. The flat Earth
concept resurfaced now and again in the Middle Ages, sometimes on religous grounds, but it is safe to say that mankind has known
for 2000 years that we live on a sphere.
We know also that it is not a perfect sphere: the diameter from pole to pole is shorter than the diameter at the equator. The
difference is small: the equatorial diameter is about 12,700 kilometers, and the pole to pole diameter is only about 40 km
shorter.
|
The reason for this difference is the Earth's rotation, wich creates a centrifugal force perpendicular to the rotation axis. If
the Earth consisted of solid material, then there would be no effect on the shape. Suppose the Earth was like a solid billiard
ball. The rotation would put a strain on the material but there would be no deformation. Our Earth has
a molten interior, it has tectonic plates on the thin crust that can move slowly, and so it is certainly not a solid ball. The
Earth is "viscous" and this accounts for the slight flattening at the poles.
Because of the rotation, the Earth has an angular momentum, L. One can look at the Earth as a huge flywheel.
The energy stored in a rotating mass is L*ω/2, where ω is the rotation speed of 2π radians per day. The value for
L is 5.86.1033 kJoule.sec. To put this in perspective: if we could harness the rotational energy of the Earth,
then it would take 5.108 years to use it all up. (at the current worldwide energy use of 10,000 million tonnes of oil
equivalent per year). The snag
is that in 500 million years, the Earth would stand still!
We will be discussing what happens if the value of L changes, so keep in mind the colossal scale of the energy
associated with the Earth's rotation.
|
 |
The theoretical shape of the Earth has been studied by mathematicians over the past 4 centuries (although the
interest has waned the last 40 years or so). The list of people who have contributed to this topic sounds like an all-time
hall of fame of mathematicians: Newton (1689), Huygens (1690), Cassini (1701), Maupertuis (1732), Clairaut (1733), Euler (1740),
MacLaurin (1742), D'Alembert (1756), Lagrange (1759), Laplace (1772), Legendre (1784), Monge (1787), Poisson (1811), Gauss (1813),
Cauchy (1815), Jacobi (1834), Dirichlet (1857), Dedekind (1860), Riemann (1860), Poincaré (1885), Darwin (1906, the son of
Charles Darwin), Jeans (1917), Cartan (1924), Chandrasekhar (1960), and others.
It was Isaac Newton who first claimed that the Earth is not spherical, but "oval". Newton imagined two wells going
down to the center of the Earth: one drilled from the North Pole, and one drilled from the equator, both filled with water. The
water in the equatorial well is subject to the centrifugal force, and the water in the Polar well is not. For the two
columns of water to be in equilibrium, it follows that the equatorial well must be longer..
In what follows we will discuss the theoretical shapes the Earth could take at a higher angular momentum, through
the milestone discoveries of Colin MacLaurin, Carl Jacobi, and Henri Poincaré.
Clicking the image above will bring up a film of the Earth as we all know it, only it turns about 800 times faster than
it does in reality (otherwise the film would have to last for 24 hours for one full turn). In all the films on this page, rotation
speed is the only item that has been scaled. The dimensions have been calculated with exact formulas.
2. McLaurin's flat Earth.
 |
Setting up a mathematical model of the Earth, taking into account all its properties, is extremely complicated: the Earth has a
non-homogeneous interior, there are internal flows of the molten material, there is a relatively thin crust, etc. A mathematical
model is only feasible if the question at hand is simplified. Studying a mass of an ideal fluid (ie. with zero viscosity), floating
in the vacuum of empty space, and subject to a rotation, yields calculable results that should at least give a reasonable
indication on what would happen in reality.
In 1742, the Scotsman Colin MacLaurin published "A Treatise on Fluxions", a milestone in the history of calculus. Amidst
items for which he is better kownn (eg.the MacLaurin series), the book also contains a study on the shape of rotating bodies.
|
MacLaurin shows that, as the angular momentum increases, the Earth will get ever more flat. The shape is an ellipsoid with two equal
axes, rotating around the short axis. The ellipsoid becomes a disc with an ever increasing radius. The rotation speed first
increases, but the speed reaches a maximum and will then decrease. As the radius of the disc
continues to grow and tends toward infinity, the rotation speed will tend toward zero: L can be expressed as L=ω.I, where I is the moment of inertia. For a constant mass, the
moment of inertia of any object will get larger and larger as the object takes on a shape where a radial dimension becomes
larger and larger. Therefore the rotation speed ω must go to zero for a finite L and an ever increasing radius.
The images below show consecutive stages of the shape of the Earth as the angular momentum increases. The numbers on the
images for the rotation speed and angular momentum are dimensionless values, and thus do not represent the actual rotation
speed in radians per second or angular momentum in Joule.sec. One should look at the relative values between stages. One
point of reference is that the actual rotation speed of the Earth corresponds to a value ω of approximately 0.06, and that
the actual angular momentum corresponds to a value L of about 0.024.
The maximum rotational speed is reached when the radius is only about 20% larger than the current radius. This speed is then
about 11 times the current speed, so that our days at this point would last 2 hours and 8 minutes! Beyond that point, the days
will get longer again, as the speed decreases. However, we may not notice as now the Earth is getting flat, and depending on
where we are on the globe, the sun may never set or never rise..
In the situation of the last image on the right above, the kinetic energy of the Earth is 200 times bigger than it
currently is. The Earth is a disc with a diameter of 50,000 km, about four times the current equatorial diameter, and a Pole
to Pole distance of only about 800 km.
3. Jacobi's ellipsoidal Earth.
 |
In 1834, Carl Jacobi got interested in the problem. Through his deep knowledge of elliptic functions, he was able to
prove that there can be stable configurations that are ellipsoids, just like the MacLaurin shapes, but that these can
transition to an ellipsoid shape with 3 unequal axes. The images and movie below show the transition to the 'Jacobi ellipsoids'.
Note that, just like the MacLaurin nearly flat Earth, the speed of rotation diminishes as the excentricity of the ellipsoid
increases.
We will discuss the phenomenon of transition between the MacLaurin and Jacobi shapes in the next section. |
4. Forks in the road: bifurcations.
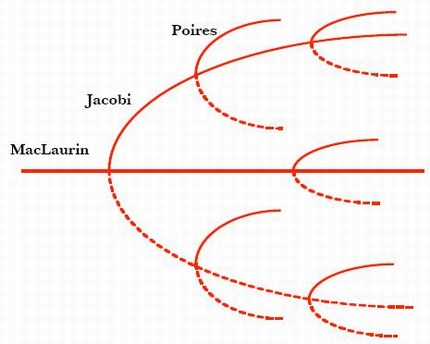
We have seen that the theoretical shape of the Earth changes to an ellipsoid as the angular momentum increases.The mathematical
formulas that describe this change are quite complicated. The fact is that, as of a certain point, they yield more than one solution.
This is illustrated below. In the picture on the left, the ball is in a stable position in the bottom of the curve. In the
picture on the right, the curve has changed its shape, and there are now two stable positions, and one instable one.
Below are two 3D versions of this situation: in the picture on the left (click on it for a movie) the surface has a single
valley on the back end, but has two symmetric valleys as we move to the front. Beyond the point where the surface has an
inflection point, the balls on the surface have two stable positions and one instable one. This is the fork in the road: a
bifurcation. In the picture on the right (click on it for a movie), the ball is at rest in the bottom of a cup.
The film shows how the surface evolves into a "Mexican hat", which has one instable position and a ring of stable
positions around it.
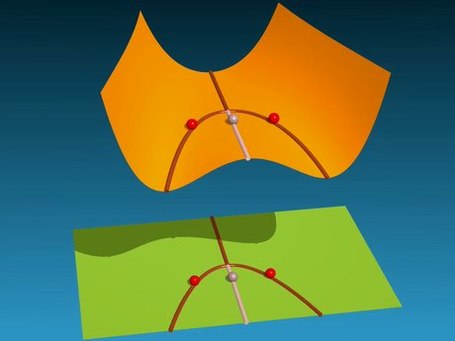 |
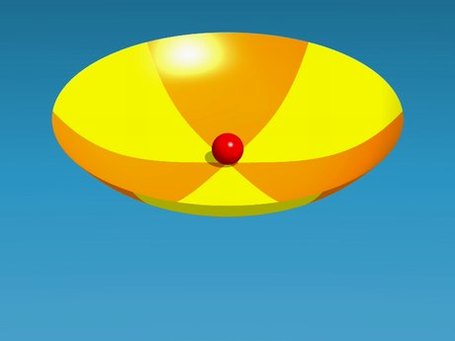 |
|
Coming back to our model of the Earth as a rotating mass of an ideal fluid with angular moment L, the "surface" is
the graph of a function U representing the interaction of the gravitational attraction and the centrifugal "repulsion" as the
total energy of the system. If the second derivative of this function is zero, we have an inflection point, and the path followed
by the shape of our "Earth" splits up: it may follow the MacLaurin route or the Jacobi route.
| 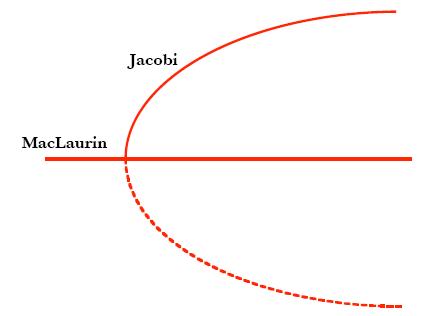 |
5. Ellipsoid geography
How would one do global positioning on an ellipsoidal world with three unequal axes? Clearly, latitude and longitude, as we
know it on our nearly spherical world, would not work.
|
Following the path of possible Jacobi ellipsoids, further bifurcations are possible, as we shall see in the next section.
This requires the calculation of the second derivative of our function U in the neighbourhood of the ellipsoids. This leads to
doing harmonic analysis on the ellipsoid, analogous to spherical harmonics on the sphere. We will then encounter
the functions of Lamé: (a<b<c)
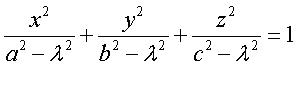
This formula describes an ellipsoid for λ<a, a one-sheeted hyperboloid for a<λ<b and
a two-sheeted hyperboloid for b<λ<c. We get a family of surfaces for a given a, b and
c that are all perpendicular to each other.
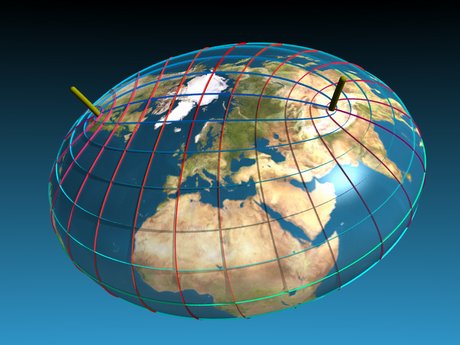
The picture on the right (click on it for a movie) shows how the two families of hyperboloids would form a latitude/longitude grid
on an elliptical world. (We have humoured the British by leaving the zero meridian going through Greenwich.)
|
 |
6. Poincaré's pear.
 |
In 1885, the great Henri Poincaré published an article in Acta Mathematica entitled "Sur l'équilibre d'une
masse fluide animée d'un mouvement de rotation" ("on the equilibrium of a fluid mass in rotation"). Here he described how
the path of the Jacobi ellipsoids encounters multiple bifurcation points. (Illustrated in the picture below on the left)
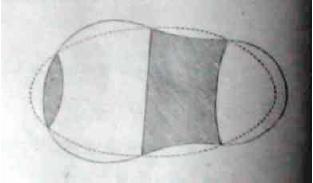
However, the shape of the mass of fluid after that bifurcation is not an ellipsoid anymore. Poincaré called it piriforme
( pear shaped ). He made a drawing of what he thought the shape would be (below on the right), which as it turns out, was wrong.
Poincaré was a genius mathematician, but had problems making accurate drawings, probably due to his bad eyesight.
|
 |
 |
|
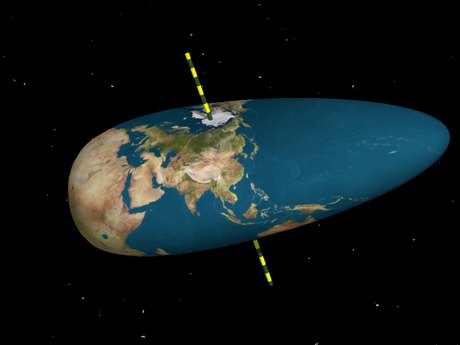
The true image stemming from his formulas is shown on the right. This is the shape after the first bifurcation on the Jacobi
path. For lack of a better name, and in honour of Poincaré, the name piriform has persisted. The movie shows
the full transition, starting from the current shape of the Earth. As the angular momentum increases,
the shape becomes an ellipsoid with two equal axes: the MacLaurin ellipsoid. It then reaches a bifurcation point and turns
into a Jacobi ellipsoid. At the first bifurcation point on the Jacobi path, we get Poincaré's 'pear'.
Poincaré also came up with the idea that this shape could explain the formation of planets. Imagine that part of the
pointed end of the 'pear' (where centrifugal forces are the highest) gets pinched off, and is sent into orbit. However, this
is a mechanism that was never confirmed by other studies.
 Movie (1.5 Mb) Movie (1.5 Mb)
|  |
7. Closing remarks.
Poincaré's paper of more than a hundred years ago was the last major milestone in the study of this topic. Chandrasekhar
wrote on Poincaré's work: "The grand mental panorama that was thus created was so intoxicating that those following
Poincaré were not to recover from its pursuit...and at this point the subject quietly went into a coma."
On the other hand, it seems that good math breeds new good math and science in general: The principle of bifurcation has
become an important concept in science. Catastrophe theory for instance, pioneered by R.Thom in the 1960's, studies
bifurcations between different equilibria, and has been applied to a wide variety of fields: from the study of a dripping faucet
to the dynamics of the capsizing of ships.
There has been no recent work on the theoretical shape of an Earth that has a higher angular momentum. On the other hand, the
study of the actual shape of the Earth, Geodesy, is a well-practised branch of geology.
Nevertheless, it might be a good idea to try and produce a real Poincaré pear shape. If NASA is running out of ideas
for test work during space missions, then this good be a good candidate.
8. Reference and further reading.
Vincent Deparis Quelle est la forme de la Terre : plate, oblongue ou aplatie aux pôles ? A historical overview
of the evolution of ideas around the shape of the earth.(in French)
An introduction to Geodesy.
Isaac Todhunter: A history of the mathematical theories of attraction and the figure of the earth., published in 1873, so
before the work of Poincaré. Available as an online book at the Gallica
online library
| |



