 | Flat Earth Nonsense
The so-called 'flat Earth doctrine' debunked in a couple of easy, verifiable steps.
Added on 2018-03-28 |
| 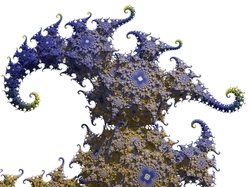 | 3D Kleinian escape time
Images made with an escape time algorithm. All images were created in Ultrafractal.
Added on 2017-09-20 |
|
| 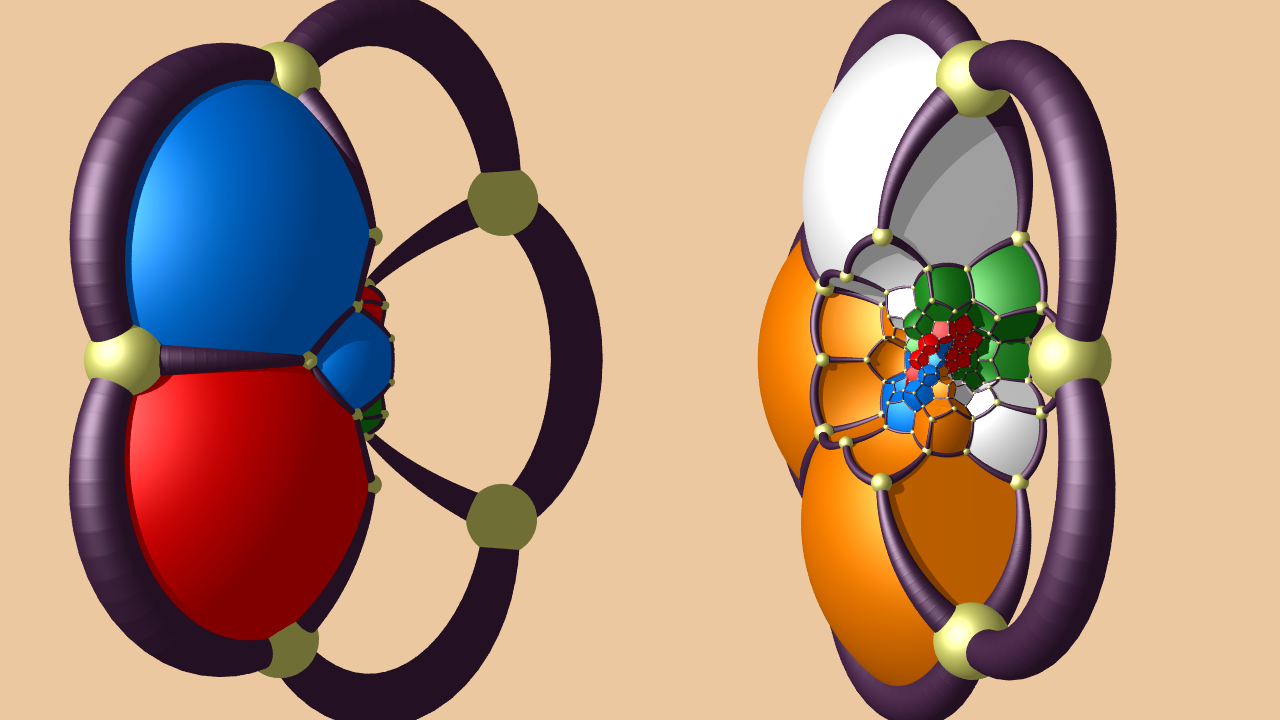 | Dodecahedral tesselation of the hypersphere
A dissection of the 120 cell in twelve rings of 10 dodecahedra. Two sets of six rings form 2 solid interlocked tori. The film starts by showing the 600 cell, the dual of the 120 cell.
Added on 2016-02-21 |
|
| |
| |
| 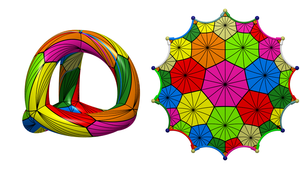 | The Klein Quartic II
The transition from a hyperbolic 14-gon to a genus 3 surface, while preserving the tiling by 24 heptagons.
Added on 2016-02-16 |
|
 | The Klein Quartic I
How this hyperbolic tiling can be folded into a genus 3 surface.
Added on 2016-02-16 |
| |
| |
 | Multiple Klein bottles
Linked Klein bottles. Note that the number of "bottles" needs to be uneven in order to have a non-orientable surface.
Added on 2016-02-16 |
| 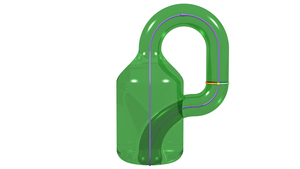 | The Klein bottle
Construction of a Klein bottle by joining the edges of a rectangle.
Added on 2016-02-16 |
|
| 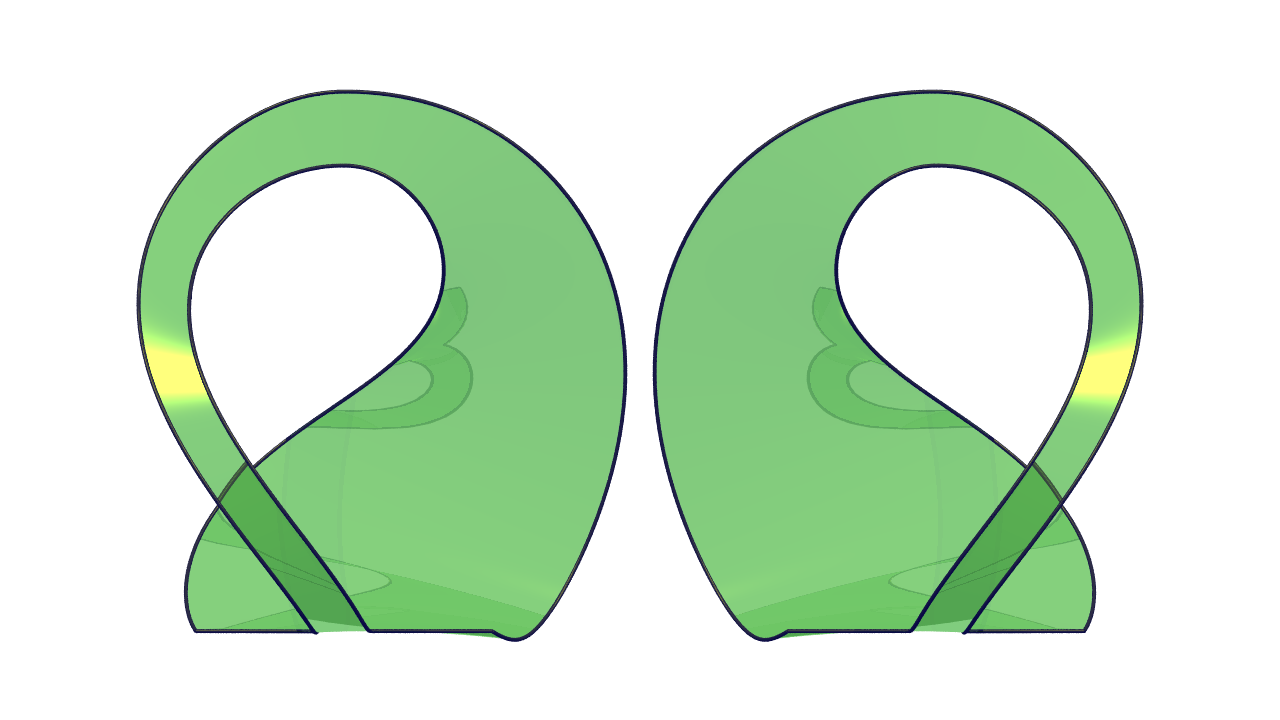 | Moebius-Klein
Two Moebius strips make a Klein bottle
Added on 2016-02-16 |
|
 | Vases
A collection of virtual vases, created by inverse stereographic projection of different patterns on the spherical surface of the vase.
Added on 2013-12-05 |
| |
|  | Mandelbrot flight #2
A spiraling flight towards a tiny area of the Mandelbrot set.
Made in Ultrafractal.
Added on 2013-09-04 |
|
 | Mandelbrot flight #1
A flight over a tiny area of the Mandelbrot set.
Made in Ultrafractal.
Added on 2013-09-01 |
|  | Newton z^4-1
A flight over a 3D Newton fractal (equation z^4-1=0).
Done entirely in Ultrafractal.
Added on 2013-08-20 |
|
 | 3D Newton test
Experimental film, done entirely in Ultrafractal.
Added on 2013-08-18 |
| |
 | Dancing circles
Iterated inversions in tangent circles create hyperbolic
tilings.
Made in Ultrafractal.
Added on 2013-06-19 |
|  | Zooms
...into the Mandelbrot set.
Made in Ultrafractal.
Added on 2013-06-19 |
|
| |
 | Mount Mandelbrot
A flight over
a 3D Mandelbrot set.
(made in Fragmentarium)
Added on 2013-06-19 |
| |
 | Hybrid 3D fractals
These were made in Ultrafractal with a combination of the Mandelbox and Mandelbulb formulas.
Added on 2013-03-14 |
|  | True 3D Kleinian groups
These limit sets of Kleinian groups were generated by three Moebius transformations with quaternion coefficients.
Added on 2013-01-05 |
|
|  | 4D Polychora
Pictures made with a kaleidoscopic method for drawing 4D polychora.
Added on 2012-06-03 |
|
| |
| |
 | Mandelbox
A special kind of 3D fractal.
Added on 2010-05-28 |
| |
|  | 3D Fractals
A small collection of 3D Mandelbrot and Julia fractals made with various formulas.
Added on 2009-12-05 |
|
 | Refraction
Un film sur la réfraction dans l'eau.
A film about refraction in water.
Made in Povray.
Added on 2009-09-17 |
|  | Hyperbolic Escher
Escher tilings converted to the hyperbolic variety.
Added on 2008-08-13 |
|
 | Sculptures
Ultrafractal and Povray working together.
Added on 2008-03-04 |
| 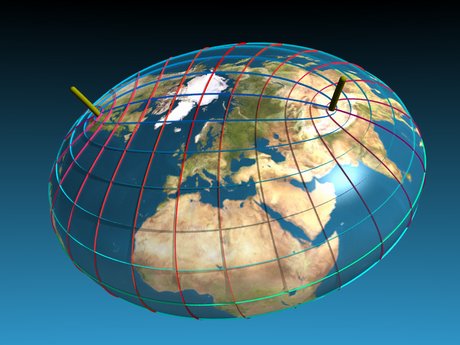 | The shape of Planet Earth
Could the Earth have been flat after all?
How about cigar shaped? Or do you prefer pear shaped?
It seems it is all possible.
Just a question of enough spin..
Added on 2006-10-24 |
|
 | Knots and dynamics
A collaboration with Prof. Etienne Ghys of the Ecole Normale Supérieure de Lyon, containing material presented at the International Congress of Mathematicians (Madrid, August 2006)
Added on 2006-08-23 |
|  | Knots and dynamics animations.
A collection of animations where one can see what a matrix looks like in four dimensions, how to make spaghetti using a 'horocycle', and more.. .
Added on 2006-08-23 |
|
 | The Droste effect
A collection of images and animations, made with a "Droste effect" image transformation.
Added on 2006-04-17 |
|  | Escher tilings
A collection of tilings, based on the work of M.C.Escher.
Added on 2006-04-16 |
|
| |
| |
| |
| |
 | Doyle spirals
Hexagonal circle packings in the plane and in 3D
Added on 2005-03-02 |
|  | Strip Geometry
These images use an algorithm that draws touching circles in a strip that stretches to infinity.
In some images this infinite strip was inverted into one circle.The algorithm is based on a paper by Professor Hans Herrmann of Stuttgart University, Germany.
Added on 2005-01-02 |
|
|  | Sphere inversions
Sphere inversion transformations are the 3D equivalent of circle inversions.
Added on 2004-11-01 |
|
 | Bubbles
These patterns are obtained by a fractal tree type algorithm.
Spheres 'grow' on a base sphere, and sprout further spheres of their own.
The different tree branches start to overlap and generate patterns.
Added on 2004-11-01 |
|  | Mathematical surfaces
A collection of classic mathematical surfaces: from the trefoil knot to the Klein bottle.
Added on 2004-09-04 |
|
|  | Sphere packings in 3D
How does one fill a sphere with smaller spheres of various sizes so that every possible void is filled?
Added on 2004-08-20 |
|
| |
| |
| |
| |
| |
| |
 | Painted Spheres
Penrose tilings, Voronoi diagrams and other things, stretched over a sphere.
Added on 2003-01-01 |
|  | Hyperbolic Tilings
The Poincaré disc: the whole world compressed in a circle.
Added on 2002-11-10 |
|
 | Celtic knots
A collection of Celtic knot patterns.
Added on 2002-10-19 |
|  | Fractal Tunnels
Deep in the crevices of Fractal valleys, there are tunnels.
Where do they lead? What lies beyond?
Added on 2002-10-01 |
|
|  | Penrose tilings
Not all images follow the 'classic' Penrose tiling rules.
Some were constructed allowing rhombs with smaller angles.
Added on 2002-08-01 |
|
 | Tiles
Simple tiling diagrams...
Added on 2002-06-01 |
|  | The Hilbert curve
The Hilbert curve is a space-filling curve.
It will eventually fill the entire plane, without ever crossing itself.
Added on 2002-06-01 |
|
 | Looms
Clifford A.Pickover in his book "Keys to Infinity" has a chapter entitled "The loom of creation",in which he describes webs spun on a circular frame. One end of the wires is tied at regular intervals, but the other end moves at a different pace.The images below are made along this principle.
Added on 2002-05-01 |
| |
| |
| |
| |
 | Strange Plants
These images are believed to be from an Earth-like planet, lightyears away.
T
Added on 2001-11-01 |
| |
 | Volvox fractals
Volvox - actually a microscopic unicellular life form that lives in colonies.
Added on 2001-10-10 |
|  | Baroque Patterns
Complicated patterns from a fairly simple fractal formula..
Added on 2001-10-06 |
|
|  | Spirals!
In all shapes, but just one size..
Added on 2001-10-04 |
|
 | Alien objects
Objects that do not seem to belong here, and can only be seen through the mathematics of fractals.
Added on 2001-10-04 |
| |
 | String fractals
Stringy objects generated by fractal formulas...
Added on 2001-10-03 |
| |
| |
| |
 | Magic Carpets
Magical shapes and colorful weavings...
Added on 2001-07-01 |
|  | The Dragoncurve
The Dragoncurve is the shape taken by a strip of paper that is folded many times.
Added on 2001-06-10 |
|
| |
| |
| |
|  | Mainstream fractals
The first collection, my first explorations in Ultrafractal
Added on 2000-10-01 |
|
|



