|
Knots and dynamicsThis page stems from a collaboration with Prof. Etienne Ghys of the Ecole Normale Supérieure de Lyon.
Prof.Ghys held a plenary lecture at the International Congress of Mathematicians in Madrid (August 2006).The professor and myself worked out the graphics for this lecture : I wrote custom algorithms in Ultrafractal to translate the math, supplied by the professor, into images and animations.
The lecture entitled "Knots and Dynamics" treats topics in fluid flow and knot theory. The graphics in these pages relate only to some aspects of these topics, as the subject matter is much broader.Some of the math used to produce these images is explained in this article.
See also this review. Back/retour |
| 
Seifert surface-tesselated
|
| 
Multi Seifert
|
| 
Seifert fibration
|
| 
Integer matrix 1
| | The projection in R^3 of the image in C^2 of a matrix with integer coefficients and determinant=1. |
| 
Integer matrix 2
| | The projection in R^3 of the image in C^2 of a matrix with integer coefficients and determinant=1.
Matrix: (162 127 , 287 225 ) |
| 
Integer matrix 3
| | The projection in R^3 of the image in C^2 of two matrices with integer coefficients and determinant=1.
Matrix: (4 1 , 7 2 ) and (2 7 , 1 4 ) |
| 
Integer matrix 4
| | The projection in R^3 of the image in C^2 of a matrix with integer coefficients and determinant=1.
Matrix: (5 2 , 747 299 ) |
|

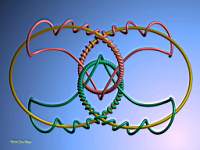
Integer matrix 5
| | The projection in R^3 of the image in C^2 of two matrices with integer coefficients and determinant=1.
Matrix: (6 5 , 403 336 ) and (336 403 , 5 6 ) |
| 
Integer matrix 6
| The projection in R^3 of the image in C^2 of two matrices with integer coefficients and determinant=1.
Matrix: (5 3 , 333 200 ) and (200 333 , 3 5 )
(Rotated 90° in C^2) |
| 
Integer matrix 7
| The projection in R^3 of the image in C^2 of two matrices with integer coefficients and determinant=1.
Matrix: (4 1 , 7 2 ) and (2 7 , 1 4 )
(Rotated 90° in C^2) |
| 
Integer matrix 8
| The projection in R^3 of the image in C^2 of two matrices with integer coefficients and determinant=1.
Matrix: (8 13 , 3 5 ) and (5 3 , 13 5 )
(Rotated 90° in C^2) |
|

Real matrix 1
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 6 5 , 403 336.6 ) |
| 
Real matrix 2
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 11.1 13.1 , 16.1 19.1 ) |
| 
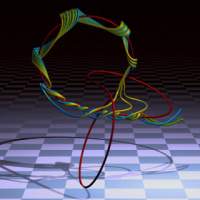
Real matrix 3
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 11.1 13.1 , 16.1 19.1 ) |
| 
Real matrix 4
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 52.2 71.12 , 41.1 56.1 ) |
|

Real matrix 5
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 5.12 7.1 , 7 10.1 ) |
| 
Real matrix 6
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 19.1 31.1 , 11.1 18.1 ) |
| 
Real matrix 7
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 5.1 7.1 , 7 10.1 ) |
| 
Real matrix 8
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 3.2 5.1 , 10.1 17.1 ) |
|

Real matrix 9
| The image of a collection of matrices with real coefficients.
|
| 
Real matrix 10
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 2 1.2 , 1.2 1 ) |
| 
Real matrix 11
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 11.1 13.1 , 16.1 19.1 ) |
| 
Real matrix 12
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 11.1 13.0 , 16.0 19.1 ) |
|

Real matrix 13
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 11.1 13.1 , 16.1 19.1 ) |
| 
Real matrix 14
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 3.2 5 , 106 177.2 ) |
| 
Real matrix 15
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 17.1 21.0 , 21.0 26.1 ) |
| 
Real matrix 16
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 5.4 7.9 , 2.9 5.4 ) |
|

Real matrix 17
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 10.1 11.0 , 12.0 13.14 ) |
| 
Real matrix 18
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 5.2 3.11 , 13.11 8.26 ) |
| 
Real matrix 19
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 13.1 20.779 , 8.04 13.1 ) |
| 
Real matrix 20
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 13.1 20.779 , 8.04 13.1 ) |
|

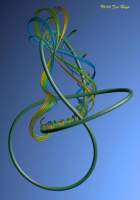
Real matrix 21
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 5.12 7.1 , 7 10.1 ) |
| 
Real matrix 22
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 97.2 115.1 , 70.1 83.1 ) |
| 
Real matrix 23
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 13.0 20.779 , 8.04 13.6 ) |
| 
Real matrix 24
| The image of a collection of matrices with real coefficients.
Based on the matrix ( 5.1 7.1 , 7 10.1 )
See also the animations page |
|
| 
Horocycle 2
|
| 
Horocycle 3
|
| 
Horocycle 4
|
|

The Lorenz template
| | An object on which a certain kind of knot can be drawn.
See also the animations page |
| 
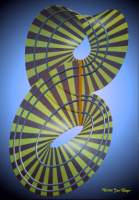
The Lorenz template
| Close-up.
The orange bar is called the 'Poincaré section'. |
| 
A variation of the Lorenz template
|
| 
deformationc002a
|
|

The Lorenz attractor
|
| 
Stable orbit 1
| A stable orbit on the Lorenz attractor.
See also the animations page |
| 
Stable orbit 2
| | A stable orbit on the Lorenz attractor |
| 
Stable orbit 3
| | Multiple stable orbits |
|

Knot deformation 1A
| | A knot, based on an integer matrix is deformed... |
| 
Knot deformation 1B
| | ...and comes to rest on the template. |
| 
deformationc007
|
| 
deformationc008
|
|
|



