Advanced geometry

Where we find Penrose, Voronoi and hyperbolic tilings..and where we have some fun with circles and spheres.We also encounter math surfaces, plane-filling curves, knot dynamics and take a mathematical look at the shape of Planet Earth.

Galleries :

Vases A collection of virtual vases, created by inverse stereographic projection of different patterns on the spherical surface of the vase. Added on 2013-12-05	4D Polychora Pictures made with a kaleidoscopic method for drawing 4D polychora. Added on 2012-06-03
Knots and dynamics A collaboration with Prof. Etienne Ghys of the Ecole Normale Supérieure de Lyon, containing material presented at the International Congress of Mathematicians (Madrid, August 2006) Added on 2006-08-23	Hyperbolic tesselations in 3D Two kinds of views of hyperbolic space. Added on 2012-06-03
Flat Earth Nonsense The so-called 'flat Earth doctrine' debunked in a couple of easy, verifiable steps. Added on 2018-03-28	Knots and dynamics animations. A collection of animations where one can see what a matrix looks like in four dimensions, how to make spaghetti using a 'horocycle', and more.. . Added on 2006-08-23
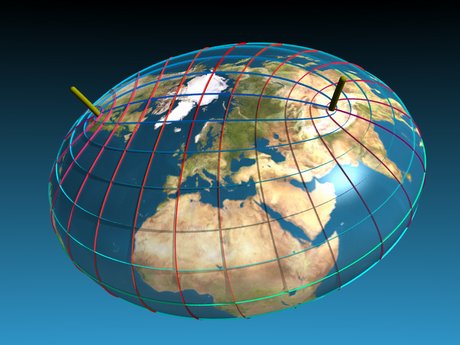The shape of Planet Earth Could the Earth have been flat after all? How about cigar shaped? Or do you prefer pear shaped? It seems it is all possible. Just a question of enough spin.. Added on 2006-10-24	Hyperbolic rings and strips Transformations of tilings in the Poincaré disc. Added on 2010-04-22
Hyperbolic animations Animated hyperbolic tilings. Added on 2005-04-18	Animations of 3D curves and surfaces Moving curves and surfaces! Added on 2005-04-18
Frivolous mathematical surfaces I don't think you will find many of these in a math textbook... Added on 2004-09-01	Penrose tilings Not all images follow the 'classic' Penrose tiling rules. Some were constructed allowing rhombs with smaller angles. Added on 2002-08-01
The Dragoncurve The Dragoncurve is the shape taken by a strip of paper that is folded many times. Added on 2001-06-10	Hyperbolic Tilings The Poincaré disc: the whole world compressed in a circle. Added on 2002-11-10
The Hilbert curve The Hilbert curve is a space-filling curve. It will eventually fill the entire plane, without ever crossing itself. Added on 2002-06-01	Painted Spheres Penrose tilings, Voronoi diagrams and other things, stretched over a sphere. Added on 2003-01-01
Fun with Circles Ford circles and circle inversions. For more information on Ford circles, visit Wikiverse Ford circle page . For more information on circle inversions, visit Wikiverse inversion page . Added on 2003-06-01	Mathematical surfaces A collection of classic mathematical surfaces: from the trefoil knot to the Klein bottle. Added on 2004-09-04
Voronoi diagrams Acknowledgments to Craig S. Kaplan , who introduced me to ornamental Voronoi designs through his paper on the subject. Added on 2002-09-22