|
| Latest galleries :  | Flat Earth Nonsense
The so-called 'flat Earth doctrine' debunked in a couple of easy, verifiable steps.
Added on 2018-03-28 |
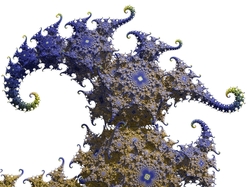 | 3D Kleinian escape time
Images made with an escape time algorithm. All images were created in Ultrafractal.
Added on 2017-09-20 |
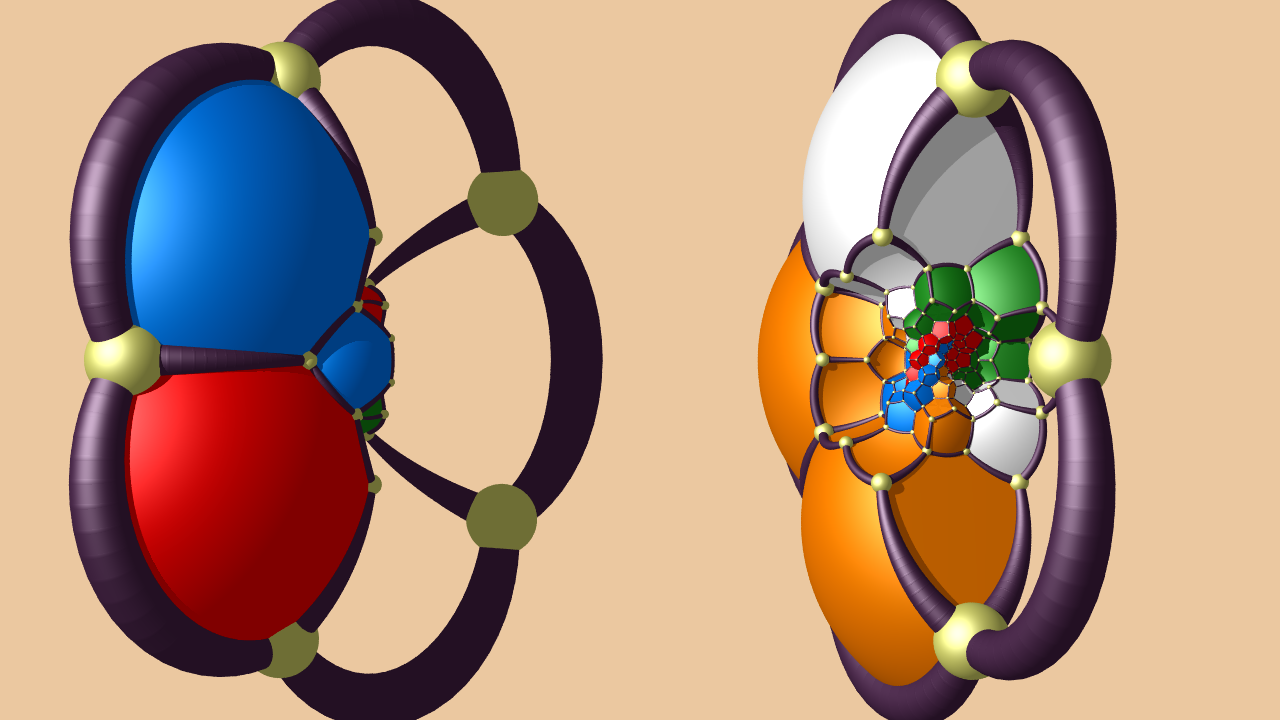 | Dodecahedral tesselation of the hypersphere
A dissection of the 120 cell in twelve rings of 10 dodecahedra. Two sets of six rings form 2 solid interlocked tori. The film starts by showing the 600 cell, the dual of the 120 cell.
Added on 2016-02-21 |
View All galleries by date | Galleries by category : | Kleinian groups
Where we enter the wonderful world first envisaged by Felix Klein. These pages where inspired by "Indra's Pearls" by David Mumford, Caroline Series and David Wright.
| | 3D inversive geometry
Where we we find ways of filling spheres with spheres and do other strange things with this simplest of all 3D objects... | | 3D Fractals
Different species of fractals in 3D... | | Circle Packings
Where we discover the art of assembling kissing circles, and find out what Doyle spirals are. | | The M.C.Escher flavoured pages
Where we find impossible geometry, tesselations and even the Droste effect. | | Advanced geometry
Where we find Penrose, Voronoi and hyperbolic tilings..and where we have some fun with circles and spheres.We also encounter math surfaces, plane-filling curves, knot dynamics and take a mathematical look at the shape of Planet Earth. | | Simple geometry
Things like Celtic knots, spirals and 'Looms". | | Fractals
Fractal images, including general 3D fractals and the Mandelbulb. | | Movies
Movie collection | | Biomorphic fractals
Biomorphic: resembling or suggesting the forms of living organisms | | Topology movies
Topics in topology |
|
| |
Copyright 2025 Jos Leys |



